い場合、 1つのバンドには2個分占有することができます。すなわちブリルアン・ゾーン の体積全体がユニットセル内の2個の電子に対応します。NaとAgは一価金属であるので、 1つのバンドに1つの電子が占有されているので、プリルアン・ゾーン中央に(b) ブリルアン・ゾーン。(c) バンド分散3。(d) 状態密度4。 *4 紛らわしいが、semimetal、halfmetal、metalloid は、すべて異なる概念。英語でも混乱しているが、 和訳すると益々ややこしくなる。 86 ギャップ ギャップ フェルミ面が、ブラッグ面に 吸い込まれて3 ため、自由電子を表すとして、 係 数を( - )にとった。 y,z に 関 しても、同様の 扱 いを後で 行 う。 ( ) 2 ( ) 2 ( ) 1 2 2 2 2 2 2 2 x k x mE x mE x x x x x x x x x x x x φ φ φ φ φ =− =−

ブリルアン ゾーンとは パリティ物理学コース クローズアップ 柳瀬章 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋
ブリルアンゾーン 意味
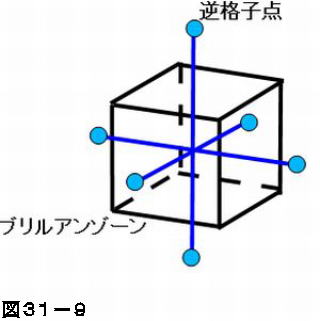
ブリルアンゾーン 意味-逆格子空間とブリルアンゾーン 逆格子空間内の単位格子(最小の繰り返 し構造)は、実空間の格子定数、以上の 波長(以下の運動量)の全電子状態を含 んでいる。この逆格子空間内の領域をブ リルアンゾーンと呼ぶ。ブルリアンゾーンその外側が第2ブリュアン・ゾーン、第3ブリュアン・ゾーン・・・ 原点を含む領域を第1ブリュアン・ゾーン、 2次元の例 垂直二等分する面で構成される領域をブリュアン・ゾーンと呼ぶ。 逆格子空間において、 の原点と他の逆格子点を結ぶ線分を k a G a k




ブリルアンゾーン境界の意味 用法を知る Astamuse
方向のL点近くのΛ線上にある。価電子帯の最 小値を示す波数(Λ線上)と価電子帯頂上の波数(Γ点)が大きく異なる為にGe は間接遷 移形半導体であり、バンドギャップは066eV である。π a − π a <ブリルアンゾーンの作り方の例:六方晶 (訂正:以前に配布した資料の六方晶の逆格子の基本ベクトル a*, b*の表記が逆) b* b c a* 100 a c 実空間、逆空間の単位格子の基本ベクトルと格子 。 実空間の単位格 たとえば ZnO はウルツ鉱型の結晶構造をもち、六方
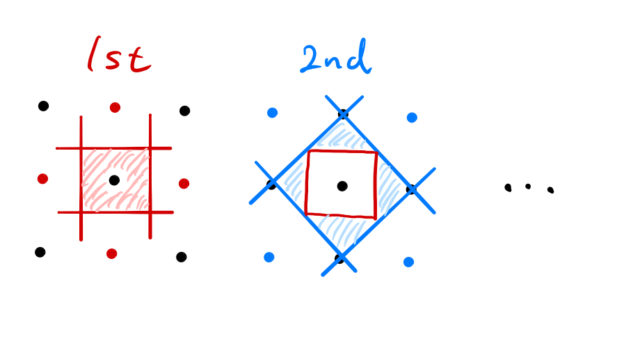
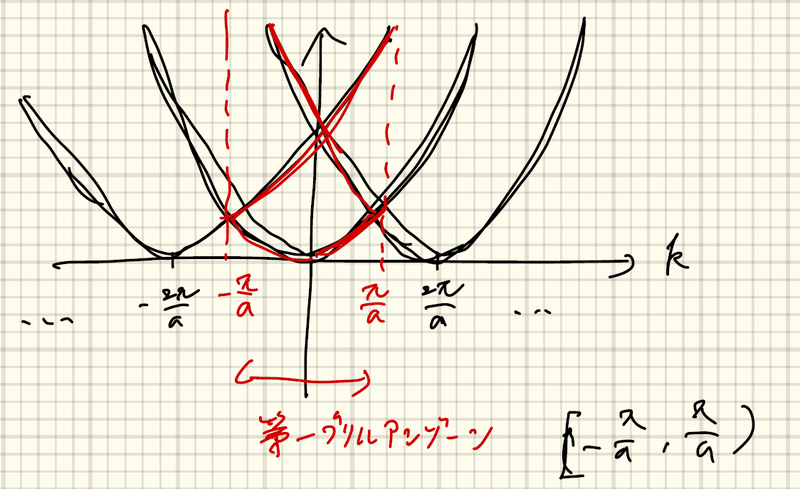
して、ミニブリルアンゾーン形成が最もドラマティック に発現する超格子の折り返しフォンモード(folded phonon mode) とミニバンド構造(miniband structure)について、ML 制御された試料を対象とした筆者らの光物性研究の成果に ついて解説する。半導体物理学 31.ブリルアンゾーン 1次元の場合、格子の周期が a a であれば、電子波の波数 k k の範囲 −π a <第2ブリルアン・ゾーン 第1ブリルアン・ゾーンに辺で 接し原点に次に近い領域を 集めたもの 原点と逆格子点の垂直2等分面で囲まれた多面体で逆格子空間を分割 第2ブリルアン・ゾーンの配置を変えると、第1ブリルアン・ゾーンと同じ形になる 612
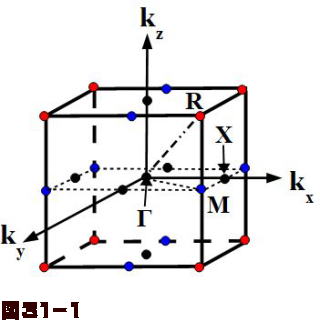
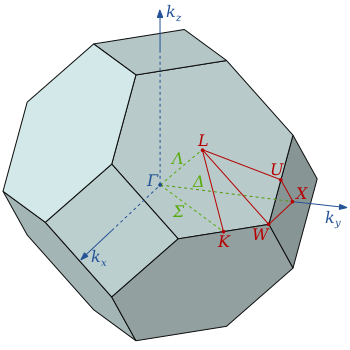
を第1ブリルアン・ゾーンと定義する。ただ単に、ブリルアン・ゾーン(Brillouin zone) と呼ばれることもある。とてもよく使われる言葉なので、よくBZ と省略される。面心 立方格子(fcc) と体心立方格子(bcc) のブリルアン・ゾーンを、図87 と図 に示す。などを参照していただく。ブリルアン・ゾーンを自分で描きたいの であればMathematicaのノートブックMakeBZnbで書ける。 g2 g1 g3 L G W K X U 図1 FCCのブリルアン・ゾーン バンド計算、DOS計算などはプログラムpwbcdで計算する。pwbcdに関する入出力ファイブリルアンゾーンの周期境界性より、チャーン数の総和はゼロでなくてはならない(ニールセン・二宮の定理)2。 よって、ブリルアンゾーン内ではモノポールと反モノポールが常にペアで存在する。 これはトポロジカルに自明になることを意味し



2
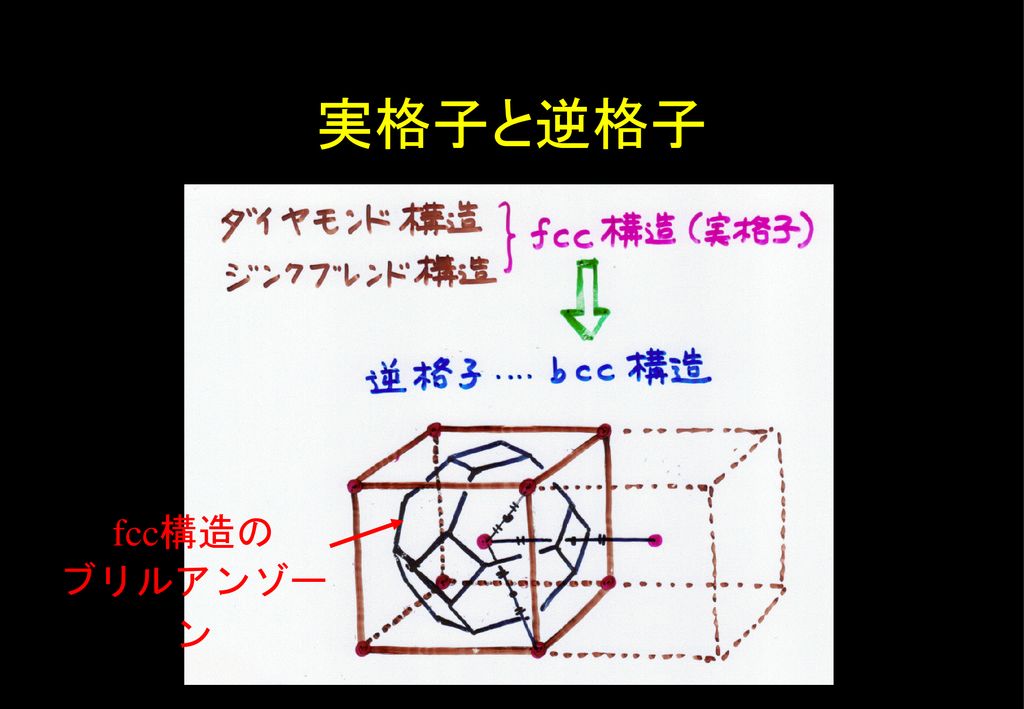



佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download
(1)結合振動子モデルと周期性 結晶中において原子は周期的に並んでおり、原子は平衡位置周りに熱振動する。周期性より、ブロッホの定理を満たす(ブロッホ電子との類似性)。 ①古典論 簡単な格子のモデルとして、同じ原子が一次元的に並んだ系を考える。第2講 -エネルギーバンドとブリルアンゾーン- 1 はじめに 前回は一様なポテンシャル中を運動する電子の振る舞 いをポテンシャル0(V(r)=0)の下でシュレーディン ガー波動方程式を解くことによって明らかにした。そ の結果、電子の波動関数は平面波ブリルアン・ゾーンの境界でエネルギーの縮退がとける 逆格子ベクトル エネルギー・バンド、禁制帯(エネルギー・ギャップ)の形成 第1ブリルアン・ゾーン 102 fcc * L X U X K W X ' / 6 Si のバンド
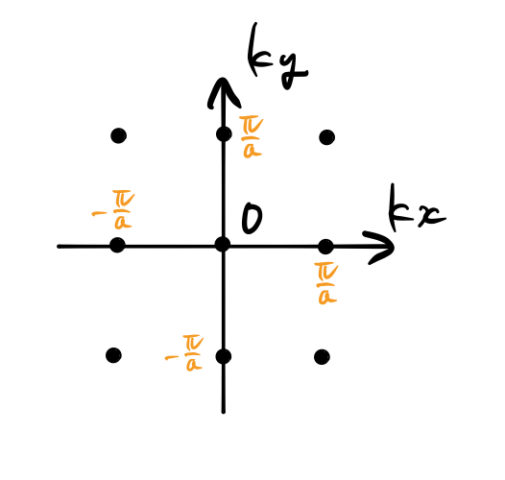



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら




ブリルアンゾーン 2次元 石くれと砂粒の世界
1 第0章 序 01 諸定数 アボガドロ(Avogadro)定数:NA = (74) 1023mol 1 ボルツマン(Boltzmann)定数:kB = (79) 10 23m2kgs 1K 1(J K 1) 気体定数 R= NAkB = (48)JK 1mol 1 プランク(Planck)定数 h= (81) 10 34m2kg=s(J s);ℏ = h=(2ˇ) 電子の静止質量:me = (11) 10 31kg 電子の素電荷 e= (98) 10 19Cることを意味する。これを第一ブリルアンゾーンという。 E ika i n ika n a a i k ik a ik a k k e e x x a → = = ⋅ ′⋅ ⋅ π π ψ ψ 2) 2 (() ・・(14) 金属 伝導帯 N L a L a = / (2 / ) (2 / ) π π 個状態数 E 伝導帯 = 個の状態数 半導体 E 価電子帯 E 伝導帯 絶縁体 図3:第一法則の辞典 ブリルアン帯(ゾーン)の用語解説 結晶格子中の波動の伝播における波数ベクトル空間内の逆格子の基本領域のこと.この領域の外の波数ベクトルは,領域内のものと等価である.




ブリルアン ゾーンとは パリティ物理学コース クローズアップ 柳瀬章 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋



2
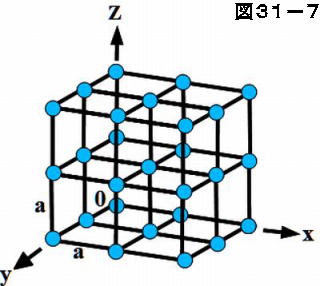
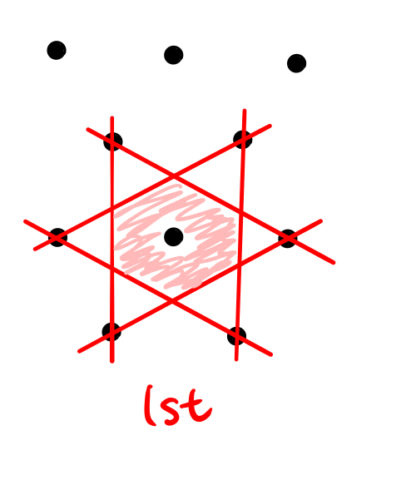
ウィグナー・ザイツセル ウィグナー・ザイツセル (WignerSeitz cell) とは、格子の格子点同士を結ぶ線分を垂直に二等分する面で囲まれた領域のことである。 結晶格子のウィグナー・ザイツセルは基本単位格子である。 ブリルアンゾーン 逆格子空間におけるウィグナー・ザイツセルをブ27.エネルギーギャップの意味 28.3次元結晶の表し方 29.3次元バンド理論 30.逆格子 31.ブリルアンゾーン 32.3次元結晶のエネルギーバンド 33.孤立した原子からの近似 半導体の性質 34.導体と絶縁体 35.伝導電子の数π a を第1ブリルアンゾーンと呼ぶことは26項で示しました。 それでは3次元の場合はどうなるでしょうか。 その前に2次元で




Android 用の 固体物理学 Apk をダウンロード
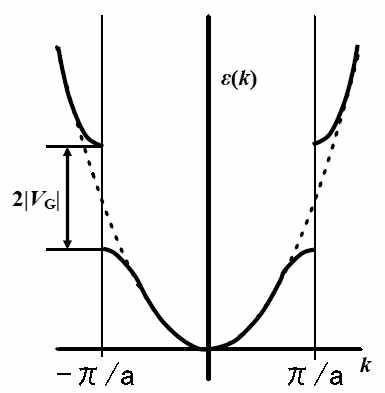



バンド描像
ンゾーンの大きさを示す。π/a は、GaAs 結晶お よびAlAs 結晶のブリルアンゾーンの大きさを 示す。 図14 図13 内の(ac)のモードのゾーンセン ター(qz=0)における格子変位パターン。(a) 第 一折返しAlAs 型LO フォノン。(b) 第一折返 しGaAs 型LO フォノン。= /D(ミニブリルアンゾーン端, 点) 図2: KP 型方程式に基づいて計算し た GaAs(34nm)/AlAs (09nm)超格子 の 電 子 と 重 い 正 孔 の ミ ニ バ ン ド エ ネルギー分散.分子∞コ 4t 中性の分子 分子間にはvan#der# Waals半径を圧縮するよ うな引力は働かない バンド幅はむし ろ小さい
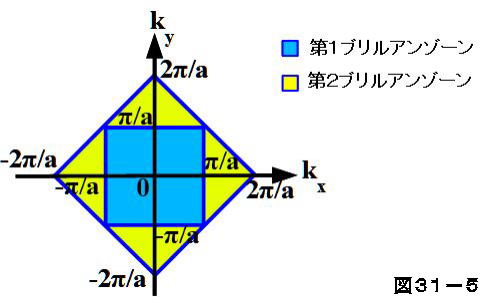



半導体物理学




ブリルアンゾーン境界の意味 用法を知る Astamuse
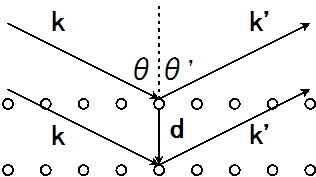
グラフェンにおいては、ブリルアン ゾーン内でギャップの閉じる点(Dirac コーン)が、同等な 点を除いて2カ所あり(K点、K'点)14)、これらは独立な2個 のDirac フェルミオンと考えられる(フェルミオンがブリルアン・ゾーンの境界にあるとき 結晶面 h がブラッグ反射して波 が作られる 2つの波 、 が干渉し 定在波を形成 ブリルアン・ゾーン ブリルアン・ゾーン第2ブリルアン・ゾーン 第1ブリルアン・ゾー ンに辺で接し原点に次に近 い領域を集めたもの 原点と逆格子点の垂直2等分面で囲まれた多面体で逆格子空間を分 割 第2ブリルアン・ゾーンの配置を変えると、第1ブリルアン・ゾーンと同じ形になる
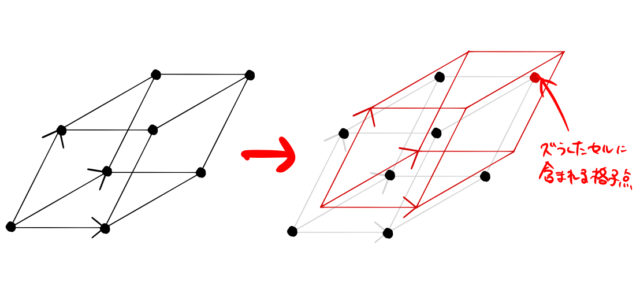



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



2
8回~9回逆格子とブリルアンゾーン・逆格子の定義 レポート5 ・逆格子の意味 代表的な逆格子 ・格子と逆格子の具体例 の計算 ・定在波の存在条件 レポート6 ・ブリルアンゾーンとその意味 ブリ結晶構造,結晶系とブラベー格子,結晶の表現方法,ブリルアンゾーン, 何故逆格子が必要か §2 結晶中の波動 ・・・・・・・・・・・・・・・・ 13 結晶における波動の量子性,音波=フォノンと格子比熱 §3



2




ブリルアン ゾーンとはの通販 柳瀬 章 紙の本 Honto本の通販ストア
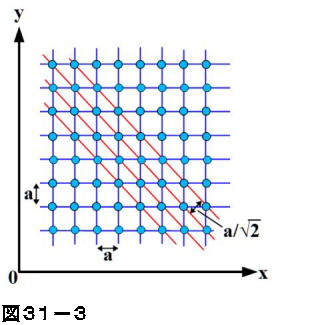



半導体物理学
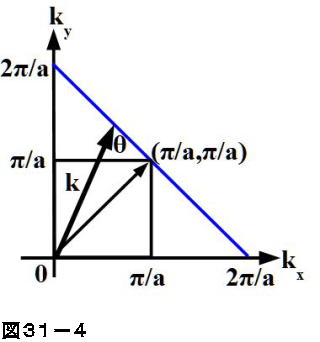



半導体物理学




14 号 半導体装置 Astamuse




固体量子41 固体物理連続講義第3回 ブリルアンゾーン Vrアカデミア Youtube
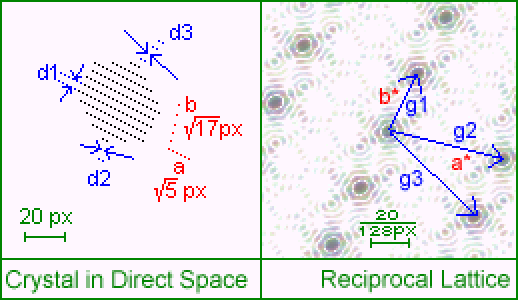



逆格子ベクトル Wikipedia
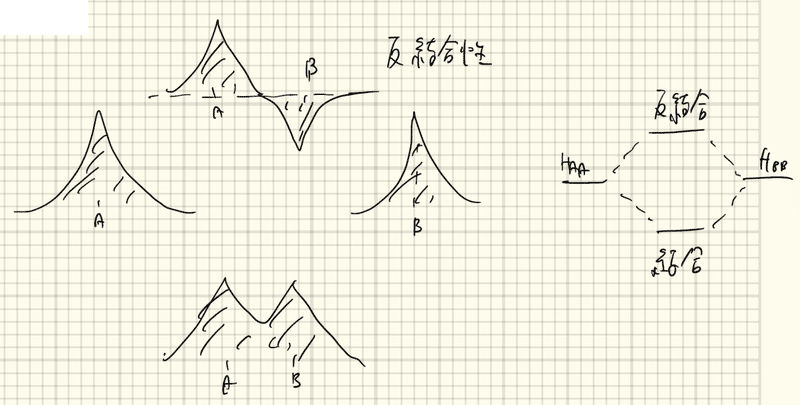



物性物理学1 3 周期ポテンシャル中の 波 としての電子 Yukishiomi Note
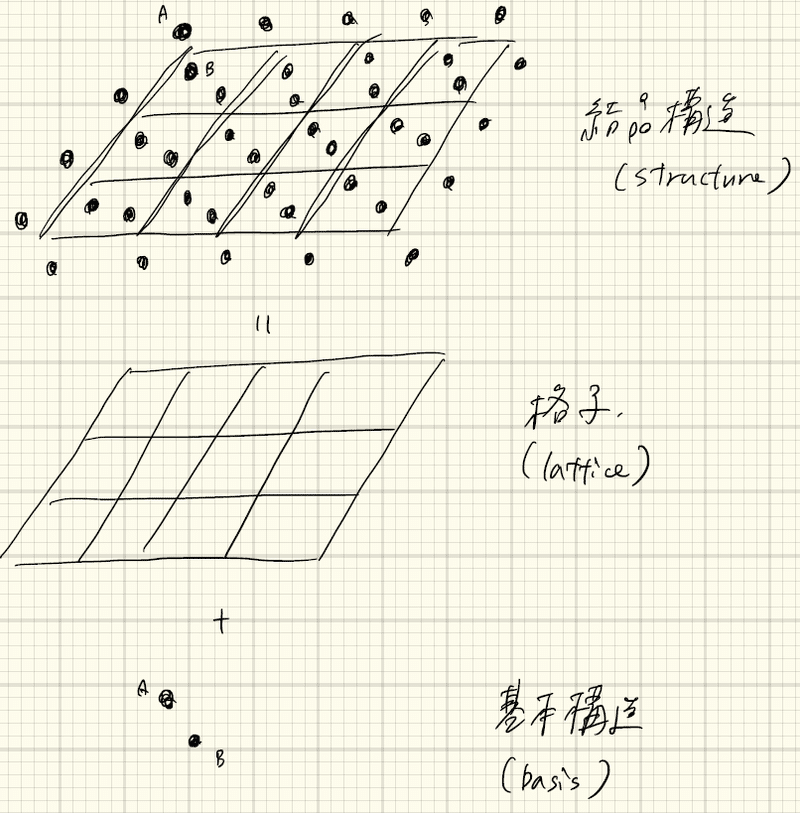



物性物理学1 2 物質の構造 Yukishiomi Note
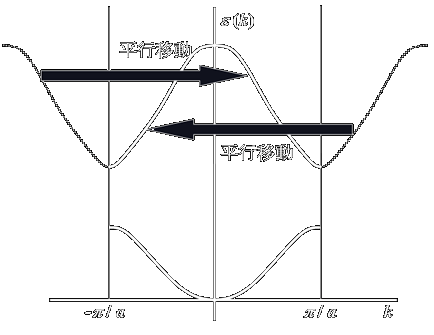



バンド描像




ブリルアンゾーン 3次元 の求め方 石くれと砂粒の世界



フェルミ面とは 物理のかぎしっぽ



Introduction Of The Electronic Structure Calculation For Experimental Researchers




2 半導体物理のおさらいi




バンド理論の勉強 武内 筑波大
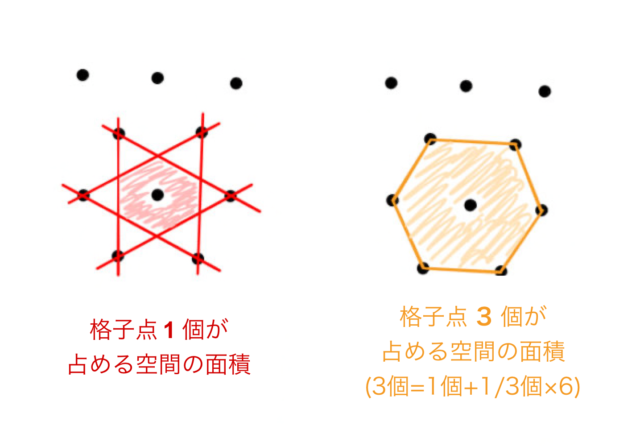



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



2




メルカリ ブリルアンゾーンとは 参考書 4 999 中古や未使用のフリマ



半導体物理学



半導体物理学




佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download




空格子近似 第2 第3及びそれ以上のブリルアンゾーン Weblio辞書



1



固体物理の質問です 全然分かりません 本当にお願いします 同種原 Yahoo 知恵袋




バンド理論 1次元 その3 石くれと砂粒の世界



2



2



2



半導体物理学



フェルミ面とは 物理のかぎしっぽ



2




運動量分解隠れ次数ギャップはuru2si2における対称性の破れとエントロピー損失の起源を明らかにする 自然通信 コミュニケーション 21



2




ウィグナー ザイツセルとブリルアンゾーン 化学徒の備忘録




ブリルアンゾーンの意味 用法を知る Astamuse



2



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



2



ブリュアンゾーン Wikipedia



2




ブリルアンゾーンの意味 用法を知る Astamuse



フェルミ面とは 物理のかぎしっぽ




バンド理論 1次元 その3 石くれと砂粒の世界



2



1



2



2



物性物理学1 3 周期ポテンシャル中の 波 としての電子 Yukishiomi Note




ブリルアン ゾーンとは パリティ物理学コース クローズアップ 柳瀬 章 洋介 長岡 本 通販 Amazon



Important Glossary For Electronic Structure Calculations




ブリルアン ゾーンとは 柳瀬章 明倫館書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




ブリルアンゾーン 2次元 石くれと砂粒の世界



2



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら



物理とか 結晶における回折条件
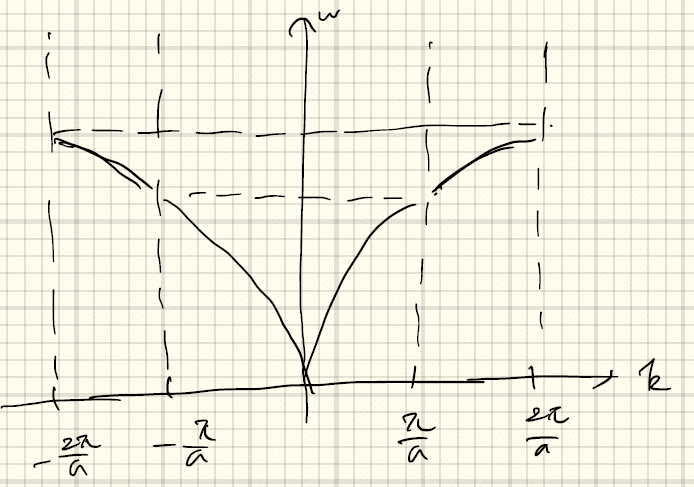



物性物理学1 4 格子振動 フォノン Yukishiomi Note




固体量子41 固体物理連続講義第3回 ブリルアンゾーン Vrアカデミア Youtube




材料選択範囲の拡大手段 その3 石くれと砂粒の世界



2




ブリルアンゾーン境界の意味 用法を知る Astamuse




ブリルアンゾーンについて 2次元で第四ブリルアンゾーンがどこを示す 物理学 教えて Goo



2




空格子近似 空格子近似の概要 Weblio辞書
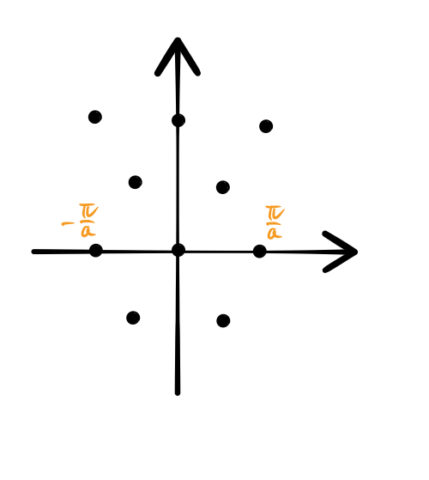



2次元のブリルアンゾーンの求め方 3次元ブリルアンゾーンの体積 ばたぱら




ブリルアンゾーン 3次元 の求め方 石くれと砂粒の世界
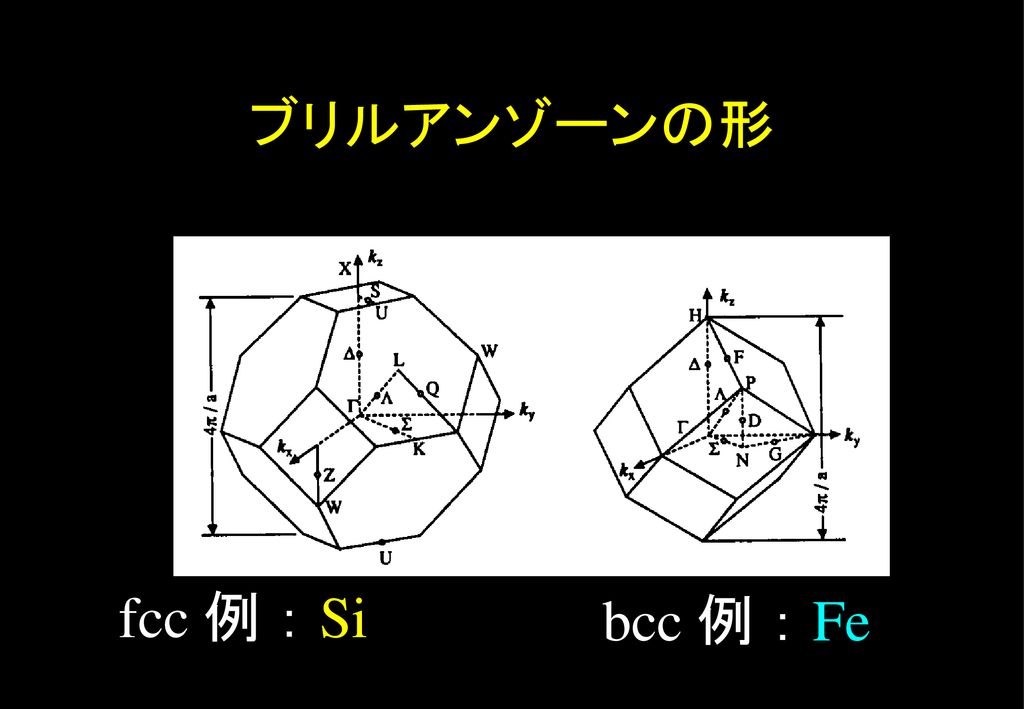



佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download
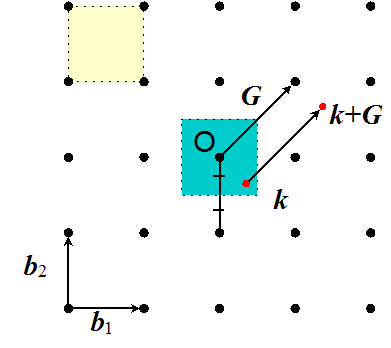



Blochの定理に関する補足とブリルアンゾーンの意味 物理とか



2



2
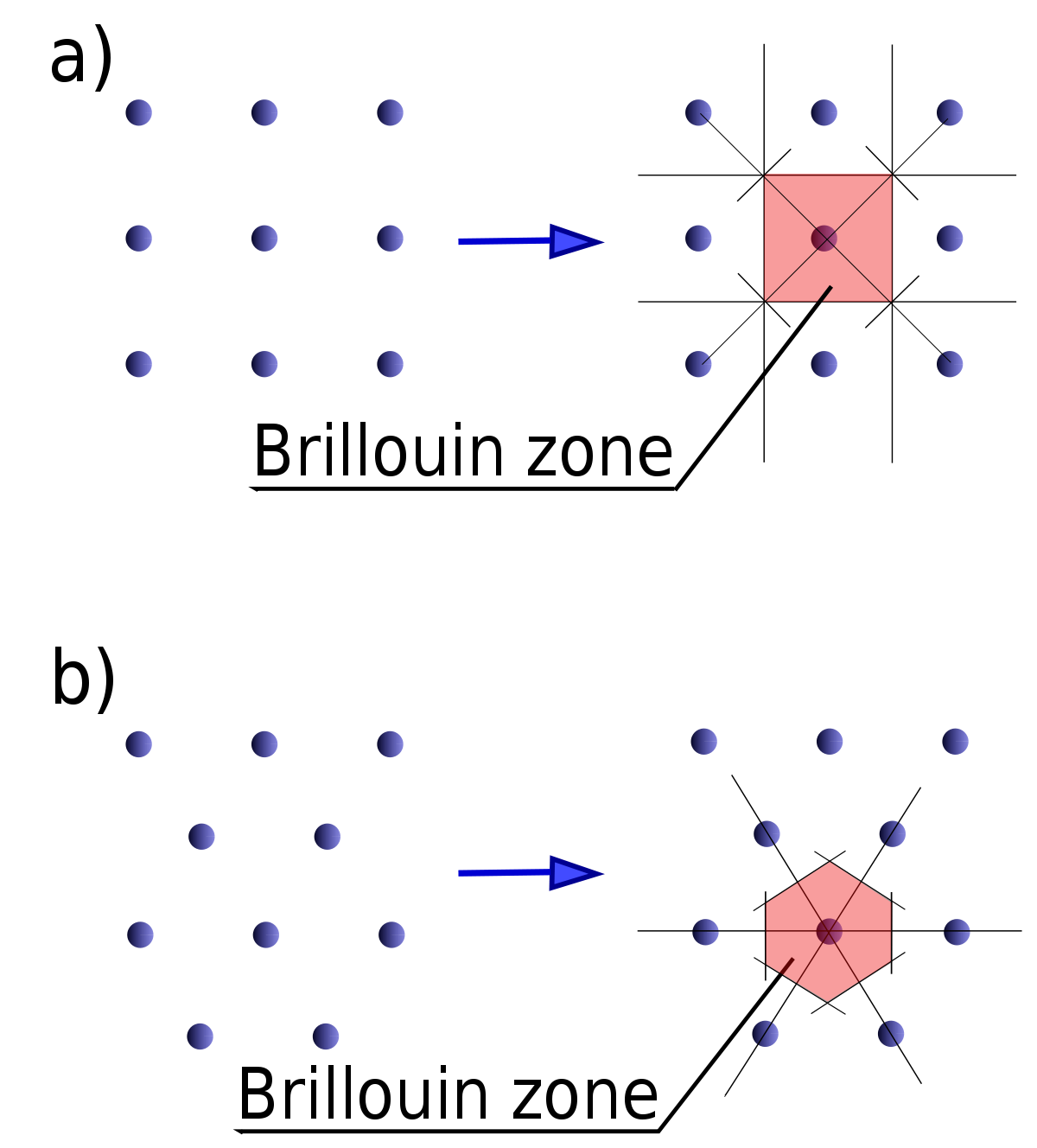



ブリュアンゾーン Wikipedia




ブリルアン ゾーンとは パリティ物理学コース クローズアップ 柳瀬 章 洋介 長岡 本 通販 Amazon



ブリルアンゾーンの対称性の高い点 Nano Exit
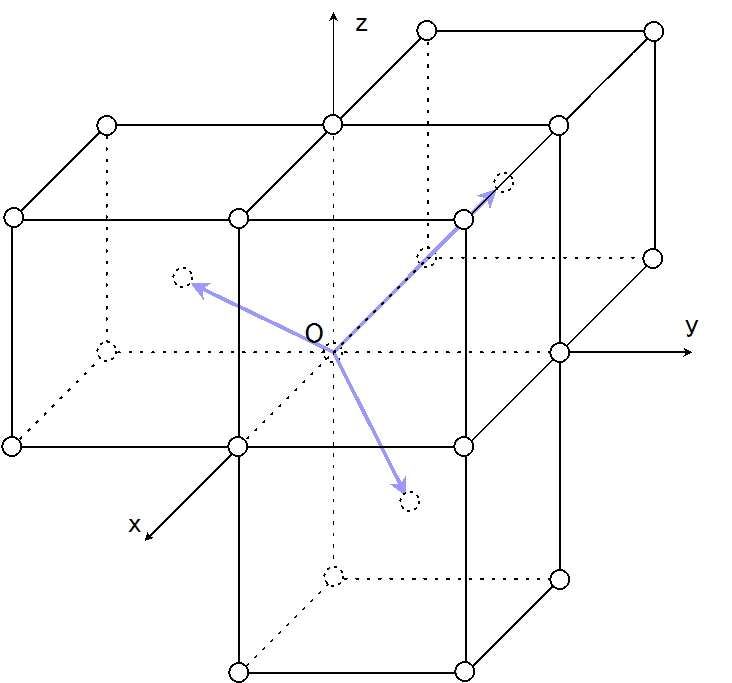



物理とか 逆格子 逆格子ベクトルの例



2



2
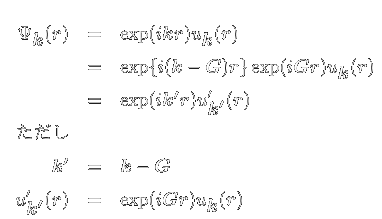



バンド描像




𝑚𝑚𝑚 Shin1n Twitter
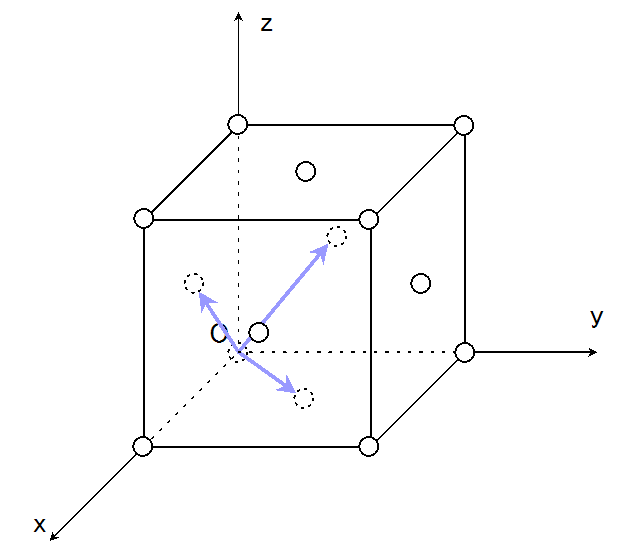



物理とか 逆格子 逆格子ベクトルの例




ブリルアンゾーンの意味 用法を知る Astamuse



2




ブリルアン ゾーンとはの通販 柳瀬 章 紙の本 Honto本の通販ストア




ブリルアン ゾーンとは 柳瀬章 明倫館書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




Woa1 赤外線吸収材料 赤外線吸収材料分散液 赤外線吸収材料分散体 赤外線吸収材料分散体合わせ透明基材 赤外線吸収透明基材 Google Patents
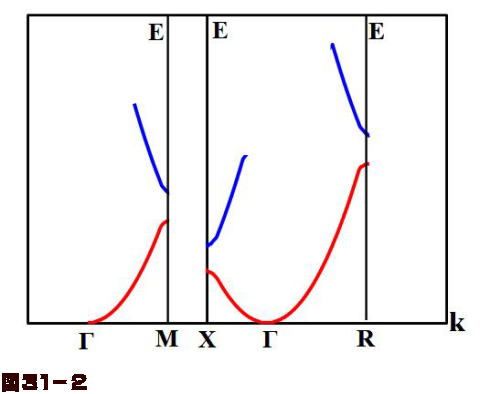



半導体物理学




ブリルアン ゾーンとは 柳瀬章 明倫館書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋



2



被害者はブリルアンゾーンの中にいる可能性が高いのは本当でしょうか Yahoo 知恵袋



2
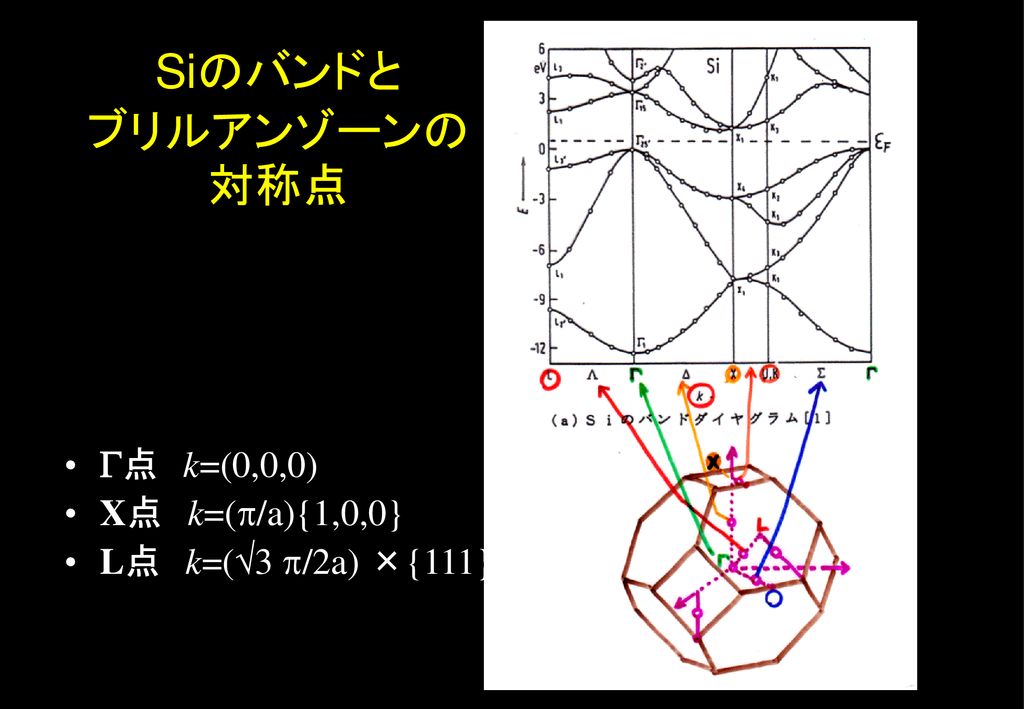



佐藤勝昭 東京農工大学 工学部物理システム工学科 Ppt Download



田仲研 Topological Insulator



0 件のコメント:
コメントを投稿